Overview - Help topics

Input parameters

• Input physics: Stellar evolution, spectral library and initial mass function
• Gaseous emission
• Galaxy types
• Initial/Total mass
• SFRFAK
• SFR0
• DECLFAK
• Metallicity

Burst parameters

• Burst strength
• Burst duration
• Burst time

Extinction

• Extinction law and maximum extinction

Cosmological parameters

• Hubble constant
• Omega-M, Omega-L, and Omega-K
• formation redshift

Output configuration

• Time evolution - Spectra
• Time evolution - Magnitudes and colours
• Time evolution - Statistics and diagnostics
• Cosmology - specs
• Cosmology - absolute magnitudes
• Cosmology - appmag
• Cosmology - attmag
• Cosmology - ecorr
• Cosmology - kcorr
• Cosmology - stat
• Normalization

Input Physics: stellar evolution, stellar spectral library and initial mass function

The choice of "Initial Mass Function" determines the full set of input physics, not only the IMF alone.

This input physics is:
1) Stellar evolution currently includes:
- stellar isochrones of the Padova group as it was in 1999, hence including TP-AGB, but not yet the later Girardi et al. 2000 or Salasnich et al. 2000 or Marigo 2001 models
- isochrones for 0.15, 0.3 and 0.45 Msun have been added from the work of Baraffe and Chabrier

2) Stellar spectral atmosphere library
described in Lejeune (1997, A&AS 125, 229) and Lejeune (1998, A&AS 130, 65) (called BaSeL 2.0)

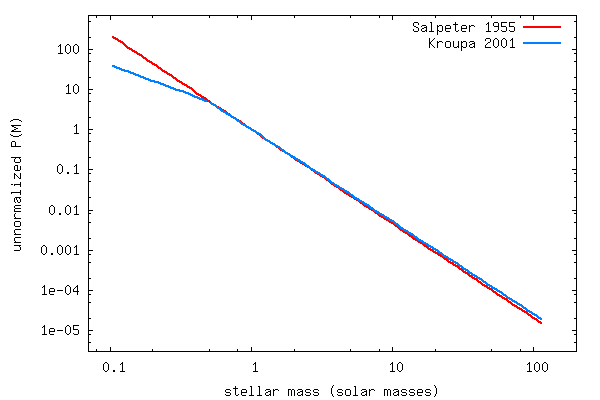
3) Initial Mass Function
Here you can choose between a range of common IMFs

• Salpeter (1955), described by P(M) = M^-a, where a=2.35.
  
• Kroupa (2001, MNRAS 322, 231), a broken power-law mass function with P(M) = M^-ai, where ai=1.3 for 0.1<M/Mo<0.5 and ai=2.3 for M/Mo>0.5.
  

The lower mass limit is defaulted to be 0.1 Mo, the upper mass-limit can be chosen to be either 100Mo or 120Mo.


(back to top)

Gaseous emission: Continuum and lines

Here you have three options to choose from:

1. No gaseous emission
   
2. Continuum emission only
   This includes bound-free emission from hydrogen and helium, free-free emission and emission from the hydrogen two-photon process.
   
3. Contiuum and line emission
   In addition to the continuum emission, this also contains emission lines for a wide range of elements. Line emission for hydrogen lines is computed on basis of atomic physics and the total number of ionizing photons. Lines of heavier elements (e.g. C, N, O) are computed from observed line-ratios relative to H-beta.
   

(back to top)

Initial/Total mass

The total mass of the galaxy, given in solar masses Msun. At the beginning all the mass is "gaseous". This changes due to star formation and stellar evolution.
Note that our models currently do not reproduce observed mass-metallicity relations, i.e. the mass is a mere scaling factor. (back to top)

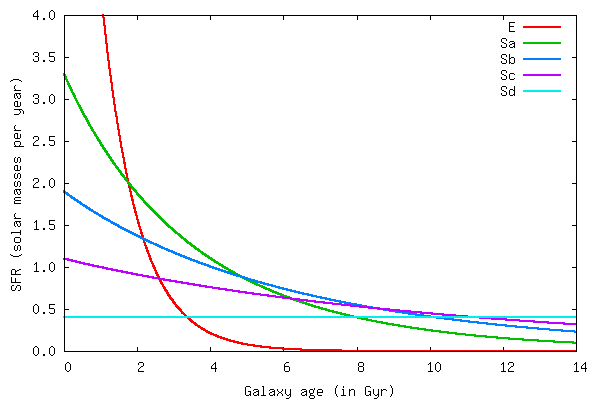
Galaxy types

The crucial factor describing and determining the galaxy type is the galaxy's star formation history (SFH).
In principal there are three different possibilities:

1. An exponentially declining star formation rate (SFR), typical for early-type galaxies, i.e. ellipticals
2. A SFR that is proportional to the available gasmass as predicted from the Kennicutt-Schmidt law. This SFH is typically observed in spiral galaxies
3. A constant SFR that is commonly used to describe the SFH of late-type spirals (Sd's)

By choosing the respective spectral galaxy type E, Sa...Sd you automatically choose the predefined parameters for the SFH of above galaxies that best represent today's observations.
If you, however, want to define your own model parameters (e.g. a different characteristic for an elliptical galaxy), you should instead choose one of the free types. The available parameters are described below (SFR, DECLFAK, SFRFAK)

The plot below shows the SFHs of the five predefined types, all normalized to a total mass of 10⁶ solar masses.

(back to top)

SFR₀ (only for free Sd)

This parameter that is only available for the galaxy type "free Sd" specifies the constant SFR in units of solar masses per year.
SFR = SFR₀ x M_tot / 10¹⁰ (back to top)

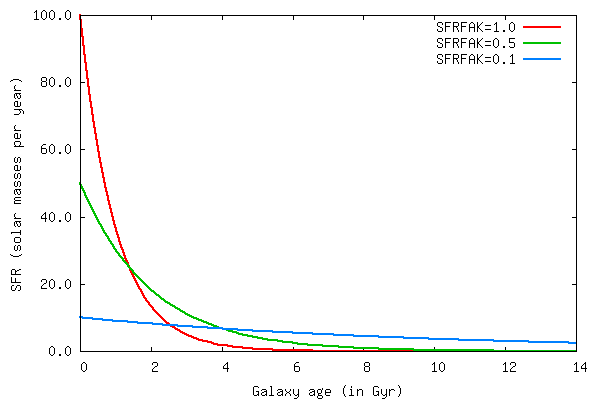
SFRFAK (only for free E & Sabc types)

This parameter specifies the star formation rate of a user-defined spiral type model. The time-dependent star formation rate in this case is given by
SFR(t) = M_gas/10⁹ x SFRFAK
This is hence equivalent to an inverse characteristic timescale for the star formation. A SFRFAK of 0.2 means a timescale of 5 Gyr, while a SFRFAK=1 means a timescale of just 1 Gyr.
(back to top)

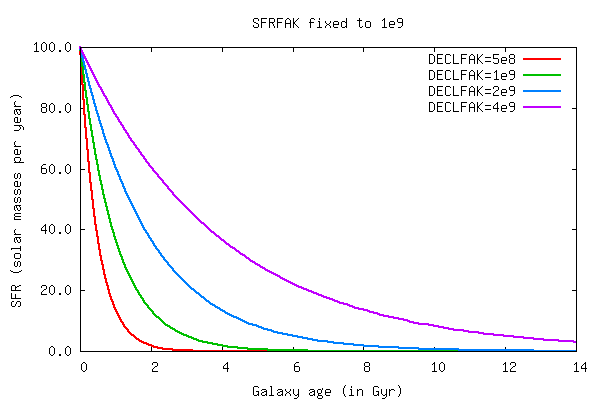
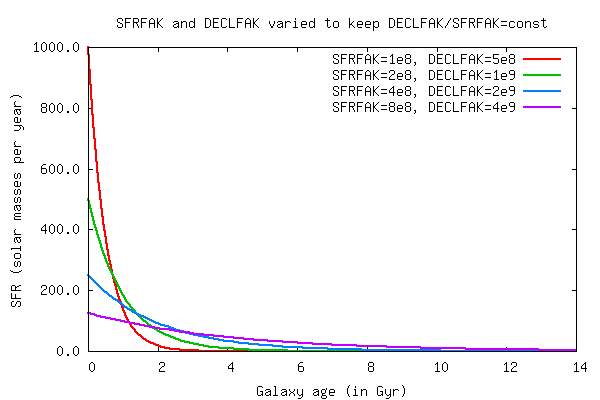
DECLFAK (Decline factor, only for free E-type)

The DECLFAK (Decline factor) parameter specified the characteristic timescale for the SFR of an elliptical galaxy. The SFR is then given by:
SFR(t) = (M_tot / SFRFAK) x exp(-t/DECLFAK) Besides the decline time the second important parameter is SFRFAK. The value of this parameter can be tuned in such a way to minimize the remaining gasmass.

(back to top)

Metallicity

All stars in the galaxy will have the same metallicity specified here, unless "chemically consistent" has been chosen. The choices are:

1. chemically consistent modelling: Switch to chemically consistent modelling.
2. [Fe/H] = -1.7, equivalent to Z = 0.0004 = 1/50 Zo
3. [Fe/H] = -0.7, equivalent to Z = 0.004 = 1/5 Zo
4. [Fe/H] = -0.4, equivalent to Z = 0.008 = 2/5 Zo
5. [Fe/H] = 0.0, equivalent to Z = 0.02 = Zo (this means solar metallicity)
6. [Fe/H] = +0.4, equivalent to Z = 0.05 = 2.5 Zo

(back to top)

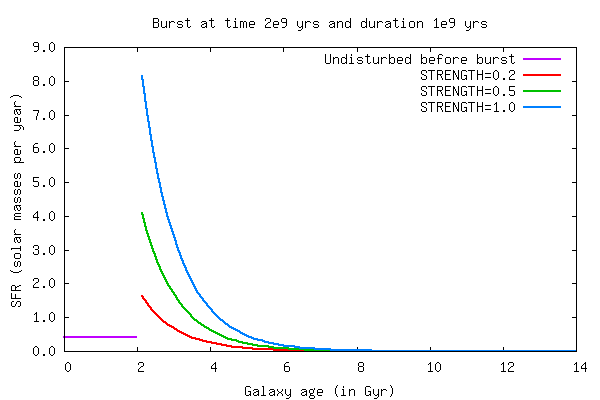
Burststrength

GALEV defines the strength of burst as the fraction of the available gas at the onset of burst that is transformed into stars during the burst:
Burststrength = Mass of formed stars / Mass of available gas
The burst strength therefore can only have values of between 0 and 1. Furthermore note that since the burststrength includes the mass of gas that is available at the beginning of the burst, the same value for the burststrength can result in different amounts of newly formed stars depending on galaxy type and time of burst. A weak burst (e.g. 20 %) early in the evolution of a Sd-type galaxy can form more stars than a strong burst (75 %) in a already old Sa galaxy.
(back to top)

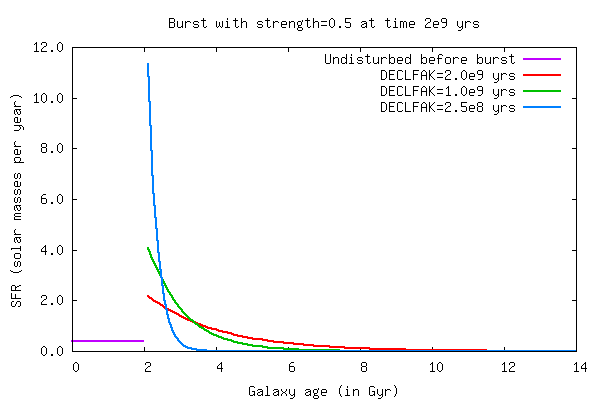
Burst duration

The parameter burst duration specifies the e-folding time for the exponentially declining SFR during the burst. Before the onset of the burst (see parameter burst time the SFR is determined by the parameters for the undisturbed galaxy.
(back to top)

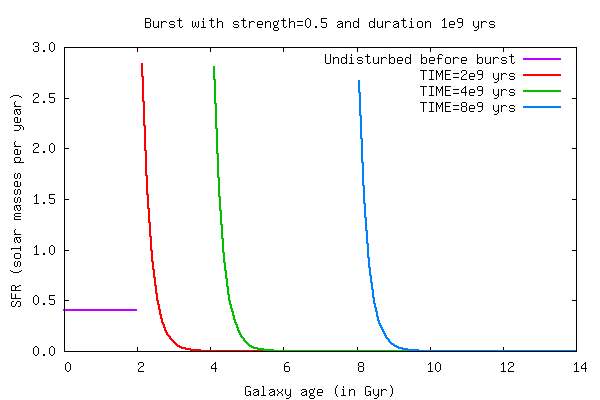
Bursttime

This parameter simply determines at which age of the galaxy the burst should occur. The value needs to be given in years, so an age of 10 Gyr should be entered as 10e9.
(back to top)

Extinction

We currently offer two different extinction laws:

1. Calzetti (2000, ApJ 533, 682)
2. Cardelli (1989, ApJ 345, 245)

You can choose a maximum extinction value and the step width between the individual extinction values. All magnitudes and spectra (depending on which output was requested, see below) are then computed for each extinction value in this range. (back to top)

Cosmology: Hubble constant, Omega-factors and formation redshifts

Here you can choose the requested cosmology. Note that if no cosmology output is requested, the values are ignored during the execution of COCOS and hence should be left at their default values.

You can change the following parameters:

• Hubble constant
• Matter content, Omega M
• Omega Lambda
• The value for Omega Curvature is fixed to be 0.00, hence limiting the cosmology to a flat universe.
• Due to the special nature of COCOS, the user furthermore has to specify a formation redshift. This is needed to convert galaxy ages to redshifts.
• One can also specify a maximum redshift. The cosmological output is then only given for redshifts smaller than the given value. This can for example be used to limit the output for models with burst or truncation to times when the burst has already occured, rejecting the evolution of the original undisturbed galaxy. Note that this only affects the cosmological output, GALEV, its spectra and the time evolution of colours are not affected by this.

(back to top)

Time evolution - Spectra

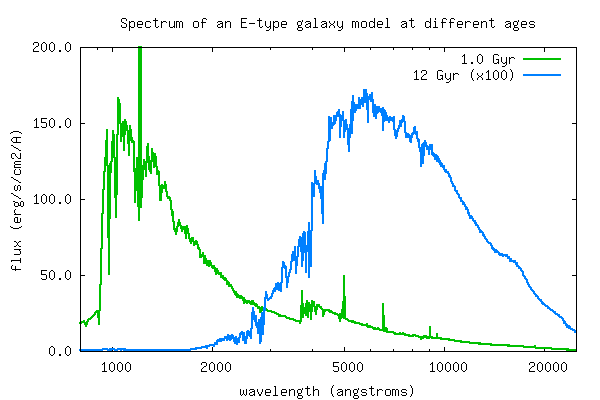(back to top)

Time evolution - Magnitudes and Colours

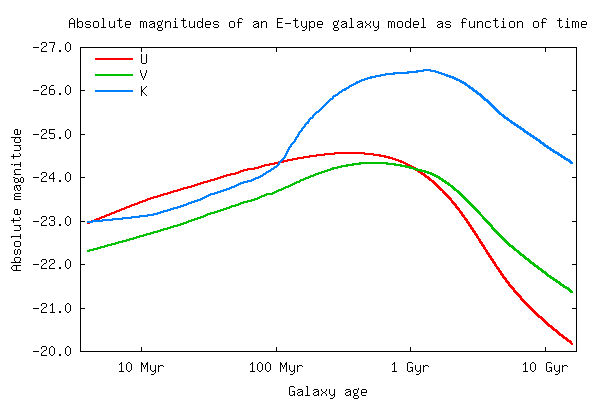
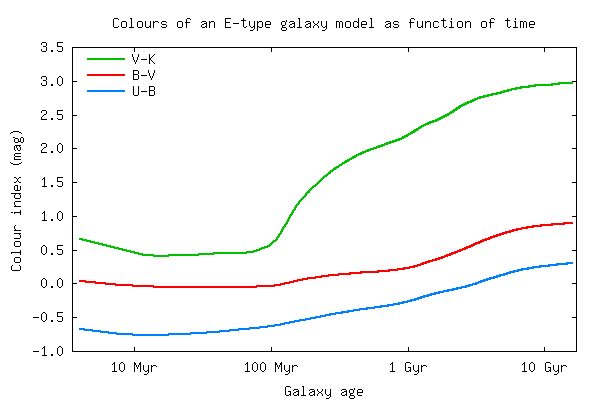(back to top)

Time evolution - Statistics & Diagnostics:
SFR, stellar and gas-mass, gaseous metallicity

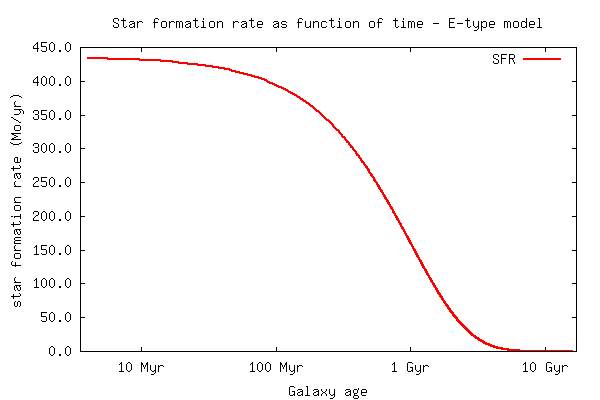
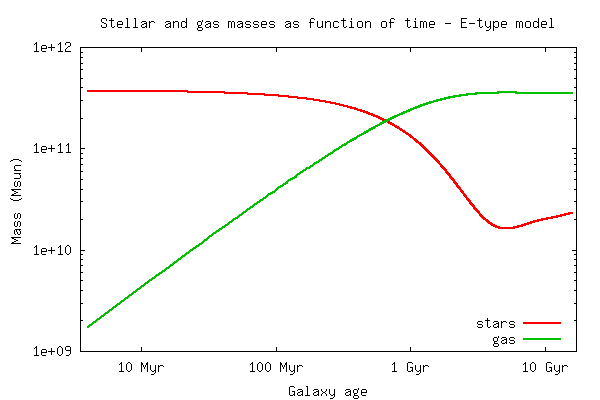
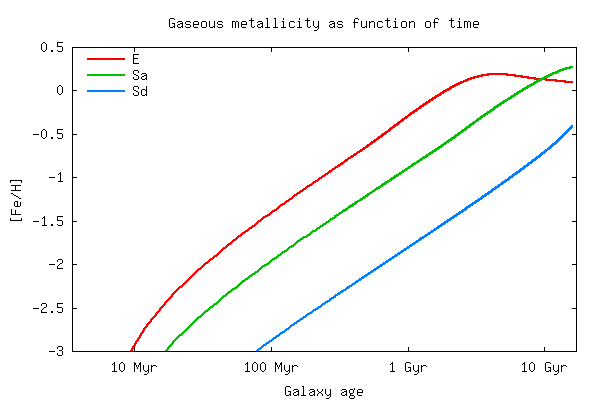(back to top)

Cosmology - specs

(back to top)

Cosmology - absolute magnitudes

(back to top)

Cosmology - appmag

(back to top)

Cosmology - attmag

(back to top)

Cosmology - ecorr

(back to top)

Cosmology - kcorr

(back to top)

Cosmology - stat

(back to top)

Normalization

(back to top)